Next: smoothingvertexnodes.f Up: Mesh refining procedure Previous: catnodes.f Contents
In this routine the quality of each element is determined. To this end the
ratio of the largest edge ![]() to the radius of the inscribed sphere is used. One can prove that the radius of the inscribed sphere of a
linear tetrahedral is three times the volume
to the radius of the inscribed sphere is used. One can prove that the radius of the inscribed sphere of a
linear tetrahedral is three times the volume ![]() divided by the sum of the area of
its faces
divided by the sum of the area of
its faces
![]() [25]. Therefore, the quality
[25]. Therefore, the quality ![]() for element
for element ![]() can be written as:
can be written as:
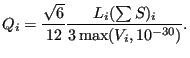 |
(715) |
The factor
![]() is such that the quality of an equilateral
tetrahedron is 1. For all other tetrahedra it exceeds 1. The larger the value,
the worse the element. The cut-off of
is such that the quality of an equilateral
tetrahedron is 1. For all other tetrahedra it exceeds 1. The larger the value,
the worse the element. The cut-off of ![]() was introduced to avoid
dividing by zero or getting a negative value.
was introduced to avoid
dividing by zero or getting a negative value.