smoothingvertexnodes.f

After smoothing a node its position $\boldsymbol{P}_i$ has changed into $\boldsymbol{P}^*_i$ satisfying:

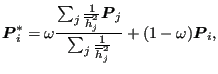$$\boldsymbol{P}^*_i = \omega \frac{\sum_{j}\frac{1}{\overline{h}_j... ...l{P}_j }{\sum_{j} \frac{1}{\overline{h}_j^2 } } + (1-\omega ) \boldsymbol{P}_i,$$ (716)

where $j$ are the neighbors of $i$, $\overline{h}_j:=(h_i+h_j)/2$ ($h_i$ is the desired edge length in node $i$) and $\omega$ is a relaxation factor taking the value of $0.5$. Defining the quality of the ball to be the quality of its worst element (i.e. highest value), a node $i$ is only smoothed if the quality of its ball after smoothing has a smaller value (i.e. is better) than before smoothing.