Next: Substructure Generation Up: Types of analysis Previous: Three-dimensional Navier-Stokes Calculations Contents
Calculations for incompressible fluids with a free surface are quite important in marine and oceanographic applications. The challenging part here is to predict the location of the free surface. A special subcategory are the problems in which the depth of the fluid is small compared to the other dimensions. In that case the general equations can be reduced to the so-called shallow water equations. These equations have a very similar behavior as the Navier-Stokes equations for compressible fluids, treated in the previous section. Linearization of these equations leads to the linear shallow water equations treated in Section 6.9.10.
Starting point for the derivation of the shallow water equations are the conservation of mass and momentum for incompressible fluids:
| (481) |
and
Now, the depth-direction of the fluid is assumed to coincide with the
![]() -direction. The momentum equation in the
-direction. The momentum equation in the ![]() -direction now reads:
-direction now reads:
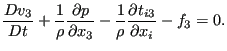 |
(483) |
The velocity in depth direction (first term) is assumed to be neglegible as well as the
viscous stress components ![]() . Furthermore, the volumetric force density
is assumed to reduce to the gravity
. Furthermore, the volumetric force density
is assumed to reduce to the gravity ![]() . Consequently, one obtains:
. Consequently, one obtains:
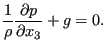 |
(484) |
Now, the depth is supposed to be composed of two contributions: a portion ![]() extending from
extending from ![]() (
(![]() ) up to
) up to ![]() , and a portion
, and a portion ![]() extending
from
extending
from ![]() up to
up to ![]() (
(
![]() ), so that the depth h
amounts to
), so that the depth h
amounts to ![]() (Figure ...). Integrating the above equation and
applying the boundary condition
(Figure ...). Integrating the above equation and
applying the boundary condition ![]() for
for ![]() , where
, where ![]() is the
atmospheric pressure, one obtains:
is the
atmospheric pressure, one obtains:
expressing the the pressure increases linearly from the surface into the depth direction.
The conservation of mass equation can be integrated in z-direction as follows:
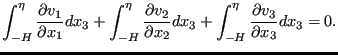 |
(486) |
Applying the Leibniz rule to the first two equations and direct integration to the last term leads to:
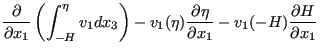 |
||
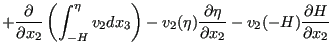 |
||
| (487) |
The velocity at the bottom is zero,
i.e.
![]() . Furthermore, a mean velocity is now defined by:
. Furthermore, a mean velocity is now defined by:
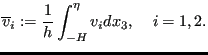 |
(488) |
This leads to:
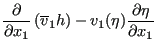 |
||
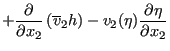 |
||
| (489) |
Now, the vertical velocity at the free surface can be written as:
leading to:
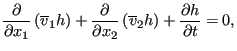 |
(491) |
since
![]() . With
. With
![]() one can also write:
one can also write:
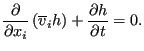 |
(492) |
This is identical to Equation 451
(conservation of mass for a compressible fluid)
in which ![]() is replaced by
is replaced by
![]() and
and ![]() by
by ![]() .
.
Integrating the momentum equation, i.e. Equation (482) in ![]() and
and ![]() direction across the depth leads to:
direction across the depth leads to:
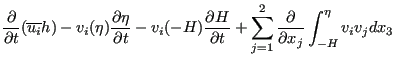 |
||
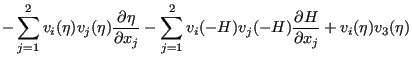 |
||
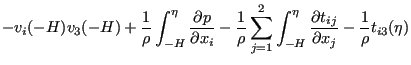 |
||
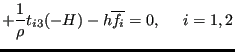 |
(493) |
Since the velocity at the bottom is zero, the third, sixth and eight term vanish. Due to the definition of the vertical velocity at the free surface, Equation (490) the second, fifth and seventh term also disappear. Due to Equation (485) the ninth term amounts to:
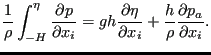 |
(494) |
The fourth term is approximated by:
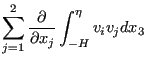 |
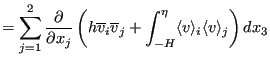 |
|
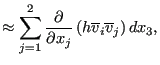 |
(495) |
and the tenth term is neglected. This leads to:
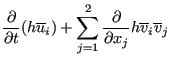 |
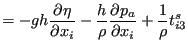 |
|
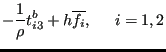 |
(496) |
Now,
![]() can also be written as:
can also be written as:
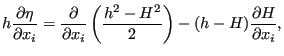 |
(497) |
leading to:
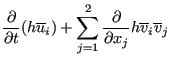 |
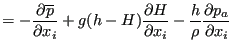 |
|
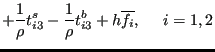 |
(498) |
were an artifical pressure
![]() has been defined by:
has been defined by:
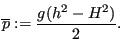 |
(499) |
Since there is no variation in depth direction and setting
![]() this also amounts to:
this also amounts to:
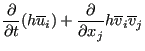 |
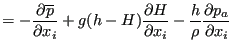 |
|
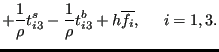 |
(500) |
This amounts to the conservation of momentum equation (447) for a
compressible fluid with the density ![]() replaced by
replaced by ![]() ,
, ![]() replaced by
replaced by
![]() ,
, ![]() replaced by
replaced by
![]() ,
, ![]() neglected and
neglected and ![]() replaced by
replaced by
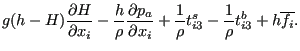 |
(501) |
The friction stress at the bottom is frequently modeled by a hydraulic resistance type formula such as
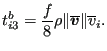 |
(502) |
The energy equation can be integrated in a similar way. I can be used of some fluid at a higher temperature is released into the flow and one would like to study the spread of the heat. The equation for incompressible flow runs:
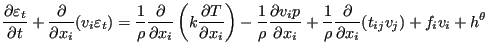 |
(503) |
Integrating from -H to ![]() yields:
yields:
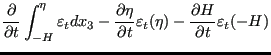 |
||
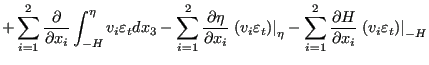 |
||
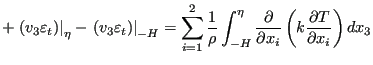 |
||
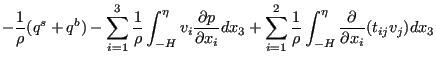 |
||
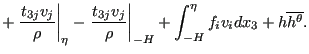 |
(504) |
Terms 3, 6 and 8 on the left hand side and term 6 on the right hand side are
zero (no velocity at the bottom and no change in time of the bottom
level). Terms 2, 5 and 7 on the left hand side disappear due to Equation
(490). The integral in the first term on left hand side is
replaced by definition by
![]() and the integral in the
fourth term is approximated by
and the integral in the
fourth term is approximated by
![]() . The variables
. The variables ![]() and
and ![]() in the second term on the
right hand side are the heat flux flowing out of the fluid at the surface and
the bottom, respecitively.
in the second term on the
right hand side are the heat flux flowing out of the fluid at the surface and
the bottom, respecitively.
Substituting the expression for the pressure,
i.e. Equation (485) into the third term on the right hand side
yields (the summation in that term really only extends from 1 to 2 since ![]() is neglegible):
is neglegible):
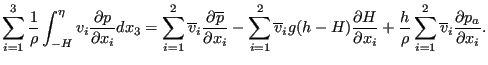 |
(505) |
The first and the fourth term on the right hand side is neglected and the eighth term is
approximated by
![]() . This finally yields:
. This finally yields:
![$\displaystyle \frac{\partial }{\partial t} (h \overline{\varepsilon_t}) + \frac...
...t [ (h \overline{\varepsilon_t} + \overline{p}) \overline{v}_i \right ] \approx$](img1699.png) |
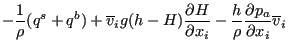 |
|
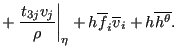 |
(506) |
This is equivalent to the energy equation for compressible fluids with ![]() replaced by
replaced by ![]() and appropriate source terms. The neglection of the stress and
conduction terms (except in
and appropriate source terms. The neglection of the stress and
conduction terms (except in ![]() -direction) can be obtained by setting
-direction) can be obtained by setting
![]() . No specific gas constant has to be defined. The parameter
COMPRESSIBLE on the *CFD card has to be replaced by the SHALLOW
WATER parameter. The pressure initial and boundary conditions have to be
replaced by conditions for
. No specific gas constant has to be defined. The parameter
COMPRESSIBLE on the *CFD card has to be replaced by the SHALLOW
WATER parameter. The pressure initial and boundary conditions have to be
replaced by conditions for
![]() . If
. If ![]() corresponds to
the fluid surface in rest, the initial conditions ususally reduce to
corresponds to
the fluid surface in rest, the initial conditions ususally reduce to
![]() .
.