Acoustics

Linear acoustic calculations in gas are very similar to heat transfer calculations. Indeed, the pressure variation in a space with uniform basis pressure $p_0$ and density $\rho_0$ (and consequently uniform temperature $T_0$ due to the gas law) satisfies

$$\nabla \cdot (- \boldsymbol{I} \cdot \nabla{p}) + \frac{1}{c_0^2} \ddot{p} = - \rho_0 \nabla \cdot \boldsymbol{f},$$ (361)

where $\boldsymbol{I}$ is the second order unit tensor (or, for simplicity, unit matrix) and $c_0$ is the speed of sound satisfying:

$$c_0=\sqrt{ \gamma R T_0}.$$ (362)

$\gamma$ is the ratio of the heat capacity at constant pressure divided by the heat capacity at constant volume ( $\gamma=1.4$ for normal air), $R$ is the specific gas constant ( $R=287 J/(kg K)$ for normal air) and $T_0$ is the absolute basis temperature (in K). Furthermore, the balance of momentum reduces to:

$$\nabla{p}=\rho_0 ( \boldsymbol{ f} - \boldsymbol{ a}).$$ (363)

For details, the reader is referred to [21] and [2]. Equation (361) is the well-known wave equation. By comparison with the heat equation, the correspondence in Table  (9) arises.

Table 9: Correspondence between the heat equation and the gas momentum equation.

heat quantity	gas quantity
T	p
$\boldsymbol{q}$	$\rho_0 (\boldsymbol{ a} - \boldsymbol{ f})$
$q_n$	$\rho_0 ( a_n - f_n)$
$\boldsymbol{\kappa}$	$\boldsymbol{I}$
$\rho h$	$- \rho_0 \nabla \cdot \boldsymbol{ f}$
$\rho c$	$\frac{ 1}{c_0^2}$

Notice, however, that the time derivative in the heat equation is first order, in the gas momentum equation it is second order. This means that the transient heat transfer capability in CalculiX can NOT be used for the gas equation. However, the frequency option can be used and the resulting eigenmodes can be taken for a subsequent modal dynamic or steady state dynamics analysis. Recall that the governing equation for solids also has a second order time derivative ([19]).

For the driving terms one obtains:

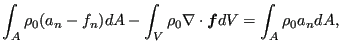$$\int_ A \rho_0 ( a_n -f_n) d A - \int_ V \rho_0 \nabla \cdot \boldsymbol{ f} dV = \int_A \rho_0 a_n dA,$$ (364)

which means that the equivalent of the normal heat flux at the boundary is the basis density multiplied with the acceleration. Consequently, at the boundary either the pressure must be known or the acceleration.