Next: The Cailletaud single crystal Up: Materials Previous: Fiber reinforced materials. Contents
The single crystal model of Georges Cailletaud and co-workers
[51][52] describes infinitesimal viscoplasticity in metallic
components consisting of one single crystal. The orientations of the
slip planes and slip directions in these planes is generally known and
described by the normal vectors
![]() and direction
vectors
and direction
vectors
![]() , respectively, where
, respectively, where ![]() denotes one of
slip plane/slip direction combinations. The slip planes and slip
directions are reformulated in the form of a slip orientation tensor
denotes one of
slip plane/slip direction combinations. The slip planes and slip
directions are reformulated in the form of a slip orientation tensor
![]() satisfying:
satisfying:
| (313) |
The total strain is supposed to be the sum of the elastic strain and the plastic strain:
| (314) |
In each slip plane an isotropic hardening variable ![]() and a kinematic
hardening variable
and a kinematic
hardening variable ![]() are introduced representing the
isotropic and kinematic change of the yield surface,
respectively. The yield surface for orientation
are introduced representing the
isotropic and kinematic change of the yield surface,
respectively. The yield surface for orientation ![]() takes the form:
takes the form:
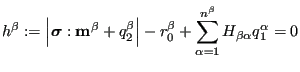 |
(315) |
where ![]() is the number of slip orientations for the material at
stake,
is the number of slip orientations for the material at
stake,
![]() is the stress tensor,
is the stress tensor, ![]() is the
size of the elastic range at zero yield and
is the
size of the elastic range at zero yield and
![]() is a
matrix of interaction coefficients. The constitutive equations for the
hardening variables satisfy:
is a
matrix of interaction coefficients. The constitutive equations for the
hardening variables satisfy:
| (316) |
and
| (317) |
where
![]() and
and
![]() are the hardening variables
in strain space. The constitutive equation for the stress is
Hooke's law:
are the hardening variables
in strain space. The constitutive equation for the stress is
Hooke's law:
| (318) |
The evolution equations for the plastic strain and the hardening variables in strain space are given by:
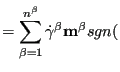 |
(319) |
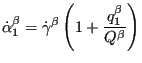 |
(320) |
and
The variable
![]() is the consistency coefficient known
from the Kuhn-Tucker conditions in optimization theory
[46]. It can be proven to satisfy:
is the consistency coefficient known
from the Kuhn-Tucker conditions in optimization theory
[46]. It can be proven to satisfy:
| (322) |
where
![]() is the flow rate along orientation
is the flow rate along orientation
![]() . The plastic strain rate is linked to the flow rate along the
different orientations by
. The plastic strain rate is linked to the flow rate along the
different orientations by
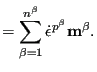 |
(323) |
The parameter
![]() in equation (321) is a
function of the accumulated shear flow in absolute value through:
in equation (321) is a
function of the accumulated shear flow in absolute value through:
| (324) |
Finally, in the Cailletaud model the creep rate is a power law function of the yield exceedance:
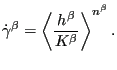 |
(325) |
The brackets
![]() reduce negative function values to zero
while leaving positive values unchanged, i.e.
reduce negative function values to zero
while leaving positive values unchanged, i.e.
![]() if
if ![]() and
and
![]() if
if ![]() .
.
In the present umat routine, the Cailletaud model is implemented for a
Nickel base single crystal. It has two slip systems, a octaeder slip
system with three slip directions ![]() in four slip planes
in four slip planes
![]() , and a cubic slip system with two slip directions
, and a cubic slip system with two slip directions ![]() in
three slip planes
in
three slip planes ![]() . The constants for all octaeder slip
orientations are assumed to be identical, the same applies for the
cubic slip orientations. Furthermore, there are three elastic
constants for this material. Consequently, for each temperature 21
constants need to be defined: the elastic constants
. The constants for all octaeder slip
orientations are assumed to be identical, the same applies for the
cubic slip orientations. Furthermore, there are three elastic
constants for this material. Consequently, for each temperature 21
constants need to be defined: the elastic constants ![]() ,
,
![]() and
and ![]() , and a set
, and a set
![]() per slip system. Apart from these constants
per slip system. Apart from these constants ![]() interaction
coefficients need to be defined. These are taken from the references
[51][52] and assumed to be constant. Their values
are included in the routine and cannot be influence by the user
through the input deck.
interaction
coefficients need to be defined. These are taken from the references
[51][52] and assumed to be constant. Their values
are included in the routine and cannot be influence by the user
through the input deck.
The material definition consists of a *MATERIAL card defining the name of the material. This name HAS TO START WITH ”SINGLE_CRYSTAL” but can be up to 80 characters long. Thus, the last 66 characters can be freely chosen by the user. Within the material definition a *USER MATERIAL card has to be used satisfying:
First line:
Following lines, in sets of 3:
First line of set:
Repeat this set if needed to define complete temperature dependence.
The crystal principal axes are assumed to coincide with the global coordinate system. If this is not the case, use an *ORIENTATION card to define a local system.
For this model, there are 60 internal state variables:
These variables are accessible through the *EL PRINT (.dat file) and *EL FILE (.frd file) keywords in exactly this order (label SDV). The *DEPVAR card must be included in the material definition with a value of 60.
Example: *MATERIAL,NAME=SINGLE_CRYSTAL *USER MATERIAL,CONSTANTS=21 135468.,68655.,201207.,1550.,3.89,18.E4,1500.,1.5, 100.,80.,-80.,500.,980.,3.89,9.E4,1500., 2.,100.,70.,-50.,400. *DEPVAR 60
defines a single crystal with elastic constants
![]() , octaeder parameters
, octaeder parameters
![]() and cubic parameters
and cubic parameters
![]() for a temperature of 400.
for a temperature of 400.