Next: Linear elastic materials for Up: Materials Previous: Linear elastic materials Contents
In [19] it is explained that substituting the infinitesimal strains
in the classical Hooke law by the Lagrangian strain and the stress by the
Piola-Kirchoff stress of the second kind does not lead to a
physically sensible material law. In particular, such a model (also called
St-Venant-Kirchoff material) does not exhibit large stresses when compressing
the volume of the material to nearly zero. An alternative for isotropic
materials is the following
stored-energy function developed by Ciarlet [17] (![]() and
and
![]() are Lamé's constants):
are Lamé's constants):
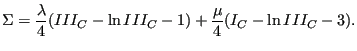 |
(295) |
The stress-strain relation amounts to (
![]() is the Piola-Kirchoff
stress of the second kind) :
is the Piola-Kirchoff
stress of the second kind) :
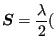 det det |
(296) |
and the derivative of
![]() with respect to the Green tensor
with respect to the Green tensor
![]() reads (component notation):
reads (component notation):
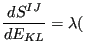 det det |
(297) |
This model was implemented into CalculiX by Sven Kaßbohm. The definition consists of a *MATERIAL card defining the name of the material. This name HAS TO START WITH ”CIARLET_EL” but can be up to 80 characters long. Thus, the last 70 characters can be freely chosen by the user. Within the material definition a *USER MATERIAL card has to be used satisfying:
First line:
Following line:
Repeat this line if needed to define complete temperature dependence.
For this model, there are no internal state variables.
Example: *MATERIAL,NAME=CIARLET_EL *USER MATERIAL,CONSTANTS=2 210000.,.3,400.
defines an isotropic material with elastic constants
![]() =210000. and
=210000. and ![]() =0.3 for a temperature of 400 (units appropriately
chosen by the user). Recall
that
=0.3 for a temperature of 400 (units appropriately
chosen by the user). Recall
that
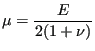 |
(298) |
and
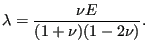 |
(299) |