Vortex

Properties: adiabatic, isentropic, asymmetric

A vortex arises, when a gas flows along a rotating device. If the inertia of the gas is small and the device rotates at a high speed, the device will transfer part of its rotational energy to the gas. This is called a forced vortex. It is characterized by an increasing circumferential velocity for increasing values of the radius, Figure 107.

Figure 107: Forced vortex versus free vortex

Another case is represented by a gas exhibiting substantial swirl at a given radius and losing this swirl while flowing away from the axis. This is called a free vortex and is characterized by a hyperbolic decrease of the circumferential velocity, Figure 107. The initial swirl usually comes from a preceding rotational device.

Figure 108: Geometry of a forced vortex

The equations for the forced and free vortex are derived from:

• The radial equilibrium of an infinitesimal volumetric element of size $r d \varphi \times dr$ subject to a pressure on all sides of the form $p(r)$ and centrifugal loading for which $\omega=C_t/r$, where $C_t$ is the local circumferential velocity. This leads to the equation

  $$\frac{1}{\rho} \frac{\partial p}{\partial r} = \frac{C_t^2}{r}.$$ (131)

  
  

  $v_r \ll C_t$ is assumed, i.e. the radial velocity is negligible w.r.t. the tangential velocity.

• the assumption that the flow is isentropic, i.e.

  $$\frac{p}{\rho ^{\kappa}} = ,$$ (132)

  
  

  e.g. equal to the value at the inner or outer position.

• the assumption that the flow is adiabatic ($T_t$ is constant).
• the assumption that the upstream and downstream nodes correspond to big reservoirs, consequently the total and static pressure as well as the total and static temperature coincide.

Integrating the differential equation (131) from $r_i$ to $r_o$ (after substitution of the isentropic assumption and separation of the variables $p$ and $r$; the index “i” stands for inner (smallest radius), “o” stands for outer (largest radius)) leads to

$$\frac{p_{t_o}}{p_{t_i}}= \left[ 1 + \frac{1}{c_p T_{t_i}} \int_{r_i}^{r_o} \frac{C_t^2}{r} dr \right]^{\frac{\kappa}{\kappa-1}}.$$ (133)

The forced vortex, Figure 108, is geometrically characterized by its upstream and downstream radius. The direction of the flow can be centripetal or centrifugal, the element formulation works for both. The core swirl ratio $K_r$, which takes values between 0 and 1, denotes the degree the gas rotates with the rotational device. If $K_r=0$ there is no transfer of rotational energy, if $K_r=1$ the gas rotates with the device. The theoretical pressure ratio across a forced vertex satisfies (substitute $C_t=K_r C_{t_i} r/r_i$ in Equation (133))

$$\left ( \frac{p_{t_o}}{p_{t_i}} \right ) _{theoretical}= \left[ 1... ... ( \frac{r_o}{r_i} \right ) ^2 -1 \right) \right ] ^ {\frac{\kappa}{\kappa-1}},$$ (134)

where $p_t$ is the total pressure, $T_t$ the total temperature and $C_{t_i}$ the circumferential velocity of the rotating device. It can be derived from the observation that the circumferential velocity of the gas varies linear with the radius (Figure 107). Notice that the pressure at the outer radius always exceeds the pressure at the inner radius, no matter in which direction the flow occurs.

The pressure correction factor $\eta$ allows for a correction to the theoretical pressure drop across the vortex and is defined by

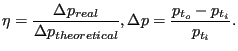$$\eta=\frac{\Delta p_{real}}{\Delta p_{theoretical}}, \Delta p = \frac{p_{t_o}-p_{t_i}}{p_{t_i}}.$$ (135)

Finally, the parameter $T_{\text{flag}}$ controls the temperature increase due to the vortex. In principal, the rotational energy transferred to the gas also leads to a temperature increase. If the user does not want to take that into account $T_{\text{flag}}=0$ should be selected, else $T_{\text{flag}}=1$ or $T_{\text{flag}}=-1$ should be specified, depending on whether the vortex is defined in the absolute coordinate system or in a relative system fixed to the rotating device, respectively. A relative coordinate system is active if the vortex element is at some point in the network preceded by an absolute-to-relative gas element and followed by a relative-to-absolute gas element. The calculated temperature increase is only correct for $K_r=1$. Summarizing, a forced vortex element is characterized by the following constants (to be specified in that order on the line beneath the *FLUID SECTION, TYPE=VORTEX FORCED card):

• $r_2$: radius corresponding to the third node in the topology of the vortex element
• $r_1$: radius corresponding to the first node in the topology of the vortex element
• $\eta$: pressure correction factor
• $K_r$: core swirl ratio
• $N$: speed of the rotating device (rad/unit of time)
• $T_{\text{flag}}$
• not used (internally: circumferential exit velocity in unit of length/unit of time (for the downstream element))

For the free vortex the value of the circumferential velocity $C_t$ of the gas at entrance is the most important parameter. It can be defined by specifying the number $n$ of the preceding element, usually a preswirl nozzle or another vortex, imparting the circumferential velocity. In that case the value $N$ is not used. For centrifugal flow the value of the imparted circumferential velocity $C_{t,theorical,i}$ can be further modified by the swirl loss factor $K_1$ defined by

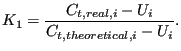$$K_1=\frac{C_{t,real,i}-U_{i}}{C_{t,theoretical,i}-U_{i}}.$$ (136)

Alternatively, if the user specifies $n=0$, the circumferential velocity at entrance is taken from the rotational speed $N$ of a device imparting the swirl to the gas. In that case $K_1$ and $U_i$ are not used and $C_{t,real,i}=N r_i$. The theoretical pressure ratio across a free vertex satisfies (substitute $C_t=C_{t,real,i} r_i/r$ in Equation (133))

$$\left ( \frac{p_{t_o}}{p_{t_i}} \right ) _{theoretical}= \left[ 1... ...eft ( \frac{r_i}{r_o} \right ) ^2 \right) \right ] ^ {\frac{\kappa}{\kappa-1}},$$ (137)

where $p_t$ is the total pressure, $T_t$ the total temperature and $C_t$ the circumferential velocity of the gas. It can be derived from the observation that the circumferential velocity of the gas varies inversely proportional to the radius (Figure 107). Notice that the pressure at the outer radius always exceeds the pressure at the inner radius, no matter in which direction the flow occurs.

Here too, the pressure can be corrected by a pressure correction factor $\eta$ and a parameter $T_{\text{flag}}$ is introduced to control the way the temperature change is taken into account. However, it should be noted that for a free vortex the temperature does not change in the absolute system. Summarizing, a free vortex element is characterized by the following constants (to be specified in that order on the line beneath the *FLUID SECTION, TYPE=VORTEX FREE card):

• $r_2$: radius corresponding to the third node in the topology of the vortex element
• $r_1$: radius corresponding to the first node in the topology of the vortex element
• $\eta$: pressure correction factor
• $K_1$: swirl loss factor (only if $n \ne 0$ and $N=0$)
• $U_i$: circumferential velocity of the rotating device at the upstream radius (only if $n \ne 0$ and $N=0$)
• $n$: number of the gas element responsible for the swirl (mutually exclusive with $N$)
• $N$: speed of the rotating device (rad/unit of time, mutually exclusive with $n$; if both $n$ and $N$ are nonzero, $N$ takes precedence)
• $T_{\text{flag}}$
• not used (internally: circumferential exit velocity in unit of length/unit of time (for the downstream element))

Example files: vortex1, vortex2, vortex3.