Next: Modifying the boundary conditions Up: Mesh refining procedure Previous: projectmidnodes.f Contents
In smoothbadmid.f the position of all subsurface bad midnodes (surface bad midnodes are not modified) is optimized by minimizing the following function F (using fminsi):
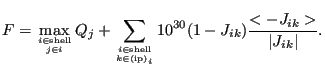 |
(719) |
In the first term of the right hand side ![]() is the quality measure for
linear tetrahedra. To this end each quadratic tetrahedral element is
subdivided into 8 linear tetrahedrons. This measure seems to be more
appropriate than using
is the quality measure for
linear tetrahedra. To this end each quadratic tetrahedral element is
subdivided into 8 linear tetrahedrons. This measure seems to be more
appropriate than using ![]() during the optimization and leads to better
shaped tetrahedrons. So basically the first term optimizes the volume of the 8
linear subtetrahedra of the quadratic tetrahedron. The second term avoids the presence of negative Jacobian determinants at the
integration points (abreviated as ip in the above formula).
during the optimization and leads to better
shaped tetrahedrons. So basically the first term optimizes the volume of the 8
linear subtetrahedra of the quadratic tetrahedron. The second term avoids the presence of negative Jacobian determinants at the
integration points (abreviated as ip in the above formula).