Next: *MODAL DYNAMIC Up: Input deck format Previous: *MEMBRANE SECTION Contents
Keyword type: step
This card is used within a step in which the *MODAL DYNAMIC or *STEADY STATE DYNAMICS procedure has been selected. There are two optional, mutually exclusive parameters: RAYLEIGH and MODAL=DIRECT (default).
If MODAL=DIRECT is selected the user can specify the viscous damping factor
![]() for each mode separately. This is the default. Direct damping is not
allowed in combination with nonzero single point constraints in a
*MODAL DYNAMIC procedure (however, in a
*STEADY STATE DYNAMICS procedure it is).
for each mode separately. This is the default. Direct damping is not
allowed in combination with nonzero single point constraints in a
*MODAL DYNAMIC procedure (however, in a
*STEADY STATE DYNAMICS procedure it is).
If RAYLEIGH is selected Rayleigh damping is applied in a
global way, i.e. the damping matrix
![]() is taken to be a linear combination of the
stiffness matrix
is taken to be a linear combination of the
stiffness matrix
![]() and the mass matrix
and the mass matrix
![]() :
:
| (644) |
The coefficients apply to all modes. The corresponding viscous damping factor
![]() for mode j amounts to:
for mode j amounts to:
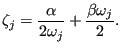 |
(645) |
Consequently, ![]() damps the low frequencies,
damps the low frequencies, ![]() damps the high
frequencies.
damps the high
frequencies.
The *MODAL DAMPING keyword can be used in any step to redefine damping values defined in a previous step.
First line:
Second line if MODAL=DIRECT is selected (or, since this is default, if no additional parameter is entered):
Second line if RAYLEIGH is selected:
Example: *MODAL DAMPING,RAYLEIGH ,,0.,2.e-4
indicates that the damping matrix is obtained by multiplying the stiffness matrix with
![]()
Example files: beamdy3, beamdy4, beamdy5, beamdy6.