Next: Hyperelastic and hyperfoam materials Up: Materials Previous: Linear elastic materials for Contents
A special case of a linear elastic isotropic material is an ideal gas for small
pressure deviations. From the ideal gas equation one finds that the pressure
deviation ![]() is related to a density change
is related to a density change ![]() by
by
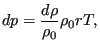 |
(303) |
where ![]() is the density at rest,
is the density at rest, ![]() is the specific gas constant and
is the specific gas constant and ![]() is the temperature in Kelvin. From this one can derive the equations
is the temperature in Kelvin. From this one can derive the equations
| (304) |
and
| (305) |
where
![]() denotes the stress and
denotes the stress and
![]() the linear strain. This means that an ideal gas can be modeled as an isotropic elastic material with
Lamé constants
the linear strain. This means that an ideal gas can be modeled as an isotropic elastic material with
Lamé constants
![]() and
and ![]() . This corresponds to a
Young's modulus
. This corresponds to a
Young's modulus ![]() and a Poisson coefficient
and a Poisson coefficient ![]() . Since the latter
values lead to numerical difficulties it is advantageous to define the ideal
gas as an orthotropic material with
. Since the latter
values lead to numerical difficulties it is advantageous to define the ideal
gas as an orthotropic material with
![]() and
and
![]() .
.