Normal contact stiffness

A node-to-face contact element consists of a slave node connected to a master face (cf. Figure 128). Therefore, it consists of $1+n_m$ nodes, where $n_m$ is the number of nodes belonging to the master face. The stiffness matrix of a finite element is the derivative of the internal forces in each of the nodes w.r.t. the displacements of each of the nodes. Therefore, we need to determine the internal force in the nodes.

Denoting the position of the slave node by $\boldsymbol{p}$ and the position of the projection onto the master face by $\boldsymbol{q}$, the vector connecting both satisfies:

$$\boldsymbol{r}= \boldsymbol{p}- \boldsymbol{q}.$$ (204)

The clearance $r$ at this position can be described by

$$r=\boldsymbol{r} \cdot \boldsymbol{n}$$ (205)

where $\boldsymbol{n}$ is the local normal on the master face. Denoting the nodes belonging to the master face by $\boldsymbol{q_i},i=1,n_m$ and the local coordinates within the face by $\xi$ and $\eta$, one can write:

$$\boldsymbol{q}= \sum _j \varphi _j(\xi ,\eta ) \boldsymbol{q_j},$$ (206)

$$\boldsymbol{m} = \frac{\partial \boldsymbol{q} }{\partial \xi } \times \frac{\partial \boldsymbol{q} }{\partial \eta }$$ (207)

and

$$\boldsymbol{n} = \frac{\boldsymbol{m} }{\Vert \boldsymbol{m} \Vert}.$$ (208)

$\boldsymbol{m}$ is the Jacobian vector on the surface. The internal force on node $p$ is now given by

$$\boldsymbol{F_p}= -f(r) \boldsymbol{n} a_p,$$ (209)

where $f$ is the pressure versus clearance function selected by the user and $a_p$ is the slave area for which node $p$ is representative. If the slave node belongs to $N$ contact slave faces $i$ with area $A_i$, this area may be calculated as:

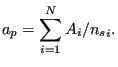$$a_p=\sum _{i=1} ^N A_i/{n_s}_i.$$ (210)

The minus sign in Equation (209) stems from the fact that the internal force is minus the external force (the external force is the force the master face exerts on the slave node). Replacing the normal in Equation (209) by the Jacobian vector devided by its norm and taking the derivative w.r.t. $\boldsymbol{u_i}$, where $i$ can be the slave node or any node belonging to the master face one obtains:

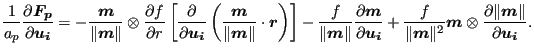$$\frac{1}{a_p} \frac{\partial \boldsymbol{F_p} }{\partial \boldsym... ...\otimes \frac{\partial \Vert \boldsymbol{m} \Vert}{\partial \boldsymbol{u_i} }.$$ (211)

Since

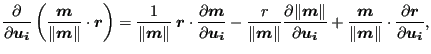$$\frac{\partial }{\partial \boldsymbol{u_i} } \left ( \frac{\bolds... ...l{m}\Vert } \cdot \frac{\partial \boldsymbol{r} }{\partial \boldsymbol{u_i} } ,$$ (212)

the above equation can be rewritten as

$$\frac{1}{a_p} \frac{\partial \boldsymbol{F_p} }{\partial \boldsymbol{u_i} } = - \left( \frac{\partial f}{\partial r } \frac{1}{\Vert \boldsymbo... ...\frac{\partial \Vert \boldsymbol{m} \Vert }{\partial \boldsymbol{u_i} } \right]$$

$$+ \frac{f}{\Vert \boldsymbol{m} \Vert } \left[ \boldsymbol{n} \ot... ...{u_i} } - \frac{\partial \boldsymbol{m} }{\partial \boldsymbol{u_i} } \right] .$$ (213)

Consequently, the derivatives which are left to be determined are $\partial \boldsymbol{m}/\partial \boldsymbol{u_i}$, $\partial \boldsymbol{r}/ \partial \boldsymbol{u_i}$ and $\partial \Vert \boldsymbol{m} \Vert / \partial \boldsymbol{u_i}$.

The derivative of $\boldsymbol{m}$ is obtained by considering Equation (207), which can also be written as:

$$\boldsymbol{m}= \sum_j \sum_k \frac{\partial \varphi _j}{\partial... ...partial \varphi_k}{\partial \eta } [ \boldsymbol{q_j} \times \boldsymbol{q_k}].$$ (214)

Derivation yields (notice that $\xi$ and $\eta$ are a function of $\boldsymbol{u_i}$, and that ${\partial \boldsymbol{q_i} }/{\partial \boldsymbol{u_j} }= \delta_{ij}\boldsymbol{I}$) :

$$\frac{\partial \boldsymbol{m} }{\partial \boldsymbol{u_i} } = \left [ \frac{\partial^2 \boldsymbol{q} }{\partial \xi^2} \times ... ...partial \eta } \right] \otimes \frac{\partial \xi }{\partial \boldsymbol{u_i} }$$

$$+ \left[ \frac{\partial \boldsymbol{q} }{\partial \xi } \times \fra... ...partial \eta} \right] \otimes \frac{\partial \eta }{\partial \boldsymbol{u_i} }$$

$$+ \sum_{j=1}^{n_m} \sum_{k=1}^{n_m} \left[ \frac{\partial \varphi_j... ...right] (\boldsymbol{I} \times \boldsymbol{q_k}) \delta_{ij}, \:\:\: i=1,..n_m;p$$ (215)

The derivatives ${\partial \xi }/{\partial \boldsymbol{u_i} }$ and ${\partial \eta }/{\partial \boldsymbol{u_i} }$ on the right hand side are unknown and will be determined later on. They represent the change of $\xi$ and $\eta$ whenever any of the $\boldsymbol{u_i}$ is changed, k being the slave node or any of the nodes belonging to the master face. Recall that the value of $\xi$ and $\eta$ is obtained by orthogonal projection of the slave node on the master face.

Combining Equations (204) and (206) to obtain $\boldsymbol{r}$, the derivative w.r.t. $\boldsymbol{u_i}$ can be written as:

$$\frac{\partial \boldsymbol{r} }{\partial \boldsymbol{u_i} }= \del... ...rtial \boldsymbol{u_i} } + \varphi_i (1 - \delta _{ip}) \boldsymbol{I} \right],$$ (216)

where $p$ represents the slave node.

Finally, the derivative of the norm of a vector can be written as a function of the derivative of the vector itself:

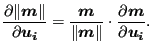$$\frac{\partial \Vert \boldsymbol{m} \Vert }{\partial \boldsymbol{... ...ol{m} \Vert} \cdot \frac{\partial \boldsymbol{m} }{\partial \boldsymbol{u_i} }.$$ (217)

The only derivatives left to determine are the derivatives of $\xi$ and $\eta$ w.r.t. $\boldsymbol{u_i}$. Requiring that $\boldsymbol{q}$ is the orthogonal projection of $\boldsymbol{p}$ onto the master face is equivalent to expressing that the connecting vector $\boldsymbol{r}$ is orthogonal to the vectors $\partial \boldsymbol{q}/ \partial \xi$ and $\partial \boldsymbol{q}/ \partial \eta$, which are tangent to the master surface.

Now,

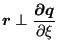$$\boldsymbol{r} \perp \frac{\boldsymbol{\partial q} }{\partial \xi }$$ (218)

can be rewritten as

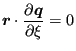$$\boldsymbol{r} \cdot \frac{\partial \boldsymbol{q} }{\partial \xi } =0$$ (219)

or

$$\left [\boldsymbol{p} - \sum_i \varphi_i (\xi ,\eta ) \boldsymbol... ...ft[ \sum_i \frac{\partial \varphi_i}{\partial \xi } \boldsymbol{q_i} \right]=0.$$ (220)

Differentation of the above expression leads to

$$\left[ d \boldsymbol{p} - \sum_i \left( \frac{\partial \varphi_i}... ...ta + \varphi_i d \boldsymbol{q_i} \right) \right] \cdot \boldsymbol{q_{\xi }} +$$

$$\boldsymbol{r} \cdot \left[ \sum_i \left( \frac{\partial^2 \varph... ...\frac{\partial \varphi_i}{\partial \xi } d \boldsymbol{ q_i} \right) \right] =0$$ (221)

where $\boldsymbol{q_{\xi }}$ is the derivative of $\boldsymbol{q}$ w.r.t. $\xi$. The above equation is equivalent to:

$$( d \boldsymbol{p} - \boldsymbol{q}_{\xi } d \xi - \boldsymbol{q}... ... } d \eta - \sum_i \varphi_i d \boldsymbol{q_i} ) \cdot \boldsymbol{q}_{\xi } +$$

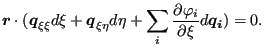$$\boldsymbol{r} \cdot ( \boldsymbol{q}_{\xi \xi} d \xi + \boldsymb... ...\eta + \sum_i \frac{\partial \varphi_i}{\partial \xi } d \boldsymbol{q_i} )=0 .$$ (222)

One finally arrives at:

$$( - \boldsymbol{q}_{\xi} \cdot \boldsymbol{q}_{\xi } + \boldsymbo... ...boldsymbol{q}_{\xi} + \boldsymbol{r} \cdot \boldsymbol{q}_{\xi \eta }) d \eta =$$

$$- \boldsymbol{q}_{\xi} \cdot d \boldsymbol{p} + \sum_i \left[ ( \... ...tial \varphi_i}{\partial \xi } \boldsymbol{r}) \cdot d \boldsymbol{q_i} \right]$$ (223)

and similarly for the tangent in $\eta$-direction:

$$( - \boldsymbol{q}_{\xi} \cdot \boldsymbol{q}_{\eta } + \boldsymb... ...ldsymbol{q}_{\eta} + \boldsymbol{r} \cdot \boldsymbol{q}_{\eta \eta }) d \eta =$$

$$- \boldsymbol{q}_{\eta} \cdot d \boldsymbol{p} + \sum_i \left[ ( ... ...ial \varphi_i}{\partial \eta } \boldsymbol{r}) \cdot d \boldsymbol{q_i} \right]$$ (224)

From this $\partial \xi / \partial \boldsymbol{q_i}$, $\partial \xi / \partial \boldsymbol{p}$ and so on can be determined. Indeed, suppose that all $d \boldsymbol{q_i}, i=1,..,n_m =\boldsymbol{0}$ and $dp_y=dp_z=0$. Then, the right hand side of the above equations reduces to $-\boldsymbol{q_{\xi}}_x dp_x$ and $-\boldsymbol{q_{\eta}}_x dp_x$ and one ends up with two equations in the two unknowns $\partial \xi / \partial p_x$ and $\partial \eta / \partial p_x$. Once $\partial \xi / \partial \boldsymbol{p}$ is determined one automatically obtains $\partial \xi / \partial \boldsymbol{u_p}$ since

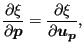$$\frac{\partial \xi }{\partial \boldsymbol{p} } = \frac{\partial \xi }{\partial \boldsymbol{u_p} },$$ (225)

and similarly for the other derivatives. This concludes the derivation of $\partial \boldsymbol{F}_p / \partial \boldsymbol{u_i}$.

Since

$$\boldsymbol{F_j}= - \varphi_j (\xi, \eta ) \boldsymbol{F_p},$$ (226)

one obtains:

$$\frac{\partial \boldsymbol{F_j} }{\partial \boldsymbol{u_i} } = -... ...ight] - \varphi_j \frac{\partial \boldsymbol{F_p} }{\partial \boldsymbol{u_i} }$$ (227)

for the derivatives of the forces in the master nodes.