Next: Arbitrary knot Up: Mathematical description of a Previous: Beam knot Contents
The expansion of a shell node leads to a set of nodes lying on a straight line. Therefore, the stretch tensor
![]() is reduced to the stretch along this line. Let
is reduced to the stretch along this line. Let
![]() be a unit vector parallel to the expansion and
be a unit vector parallel to the expansion and
![]() and
and
![]() unit vectors such that
unit vectors such that
![]() and
and
![]() . Then
. Then
![]() can be written as:
can be written as:
leading to one stretch parameter ![]() . Since the stretch along
. Since the stretch along
![]() and
and
![]() is immaterial, Equation (198) can also be replaced by
is immaterial, Equation (198) can also be replaced by
| (199) |
representing an isotropic expansion. Equation (197) can now be replaced by
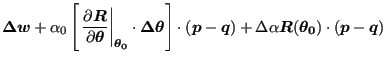 |
||
| (200) |
Consequently, a knot resulting from a shell expansion is characterized by 3 translational degrees of freedom, 3 rotational degrees of freedom and 1 stretch degree of freedom.