Change absolute/relative system

Sometimes it is more convenient to work in a relative system fixed to some rotating device, e.g. to model the flow through holes in a rotating disk. In order to facilitate this, two conversion elements were created: a relative-to-absolute element and an absolute-to-relative element. The transformation takes place at a given radius and the element has a physical length of zero. Input for this element is the circumferential velocity of the rotating device and the tangential gas velocity , both at the radius at which the transformation is to take place. The gas velocity can be specified explicitly, or by referring to an element immediately preceding the transformation location and imparting a specific swirl to the gas.

Figure 110: Vector plot of the absolute/relative velocity

Let $\boldsymbol{U}$ be the circumferential velocity of the rotating device at the selected radius, $\boldsymbol{C}$ the velocity of the gas at the same location and $C_t$ its circumferential component (Figure 110). The velocity of the gas $\boldsymbol{W}$ in the rotating system satisfies:

$$\boldsymbol{W}=\boldsymbol{C}-\boldsymbol{U}.$$ (138)

The total temperature in the absolute system is

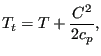$$T_t=T+\frac{C^2}{2 c_p},$$ (139)

whereas in the relative system it amounts to

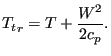$${T_t}_r=T+\frac{W^2}{2 c_p}.$$ (140)

Combining these equations and using the relationship between the length of the sides of an irregular triangle (cosine rule) one arrives at:

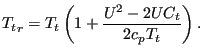$${T_t}_r=T_t \left( 1 +\frac{U^2-2 U C_t}{2 c_p T_t} \right).$$ (141)

Assuming adiabatic conditions this leads for the pressure to:

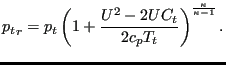$${p_t}_r=p_t \left( 1 +\frac{U^2-2 U C_t}{2 c_p T_t} \right)^{\frac{\kappa}{\kappa-1}}.$$ (142)

Depending on the size of $2 C_t$ compared to the size of $U$ the relative total temperature will exceed the absolute total temperature or vice versa. This is illustrated in Figure 111.

Figure 111: Total temperature dependence on the circumferential component of the incoming flow

Inversely, the relationships for the relative-to-absolute transformation amount to:

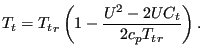$$T_t={T_t}_r \left( 1 -\frac{U^2-2 U C_t}{2 c_p {T_t}_r} \right).$$ (143)

and:

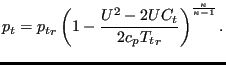$$p_t= {p_t}_r \left( 1 -\frac{U^2-2 U C_t}{2 c_p {T_t}_r} \right)^{\frac{\kappa}{\kappa-1}}.$$ (144)

These relationships are taken into account in the following way: the change in total temperature is taken care of by creating a heat inflow at the downstream node. For an absolute-to-relative change this heat flow amounts to:

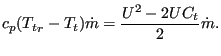$$c_p ( {T_t}_r - T_t) \dot m = \frac {U^2 - 2 U C_t}{2} \dot m.$$ (145)

The total pressure change is taken as element equation. For an absolute-to-relative change it runs:

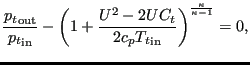$$\frac{{p_t}_{\text{out}}}{{p_t}_{\text{in}}}- \left( 1 +\frac{U^2-2 U C_t}{2 c_p {T_t}_{\text{in}}} \right)^{\frac{\kappa}{\kappa-1}}=0,$$ (146)

and for a relative-to-absolute change:

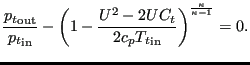$$\frac{{p_t}_{\text{out}}}{ {p_t}_{\text{in}}}- \left( 1 -\frac{U^2-2 U C_t}{2 c_p {T_t}_{\text{in}}} \right)^{\frac{\kappa}{\kappa-1}}=0.$$ (147)

For an absolute-to-relative element the input is as follows (to be specified in that order on the line beneath the *FLUID SECTION, TYPE=ABSOLUTE TO RELATIVE card):

• $U$: circumferential velocity of the rotating device at the selected radius
• $C_t$: tangential gas velocity at the selected radius
• $n$: element immediately preceding the location of the transformation

$C_t$ is taken if and only if $n=0$. In all other cases the exit velocity of the element with label $n$ is taken.

For an relative-to-absolute element the input is identical except that the type of the element is now RELATIVE TO ABSOLUTE.

Example files: moehring, vortex1, vortex2, vortex3.